Calculus early transcendentals 7th ed – Calculus Early Transcendentals, 7th Edition embarks on an extraordinary journey through the captivating world of calculus, inviting readers to unravel its intricate beauty and boundless applications. This meticulously crafted textbook unveils the fundamental concepts of calculus, empowering students to navigate complex mathematical landscapes with confidence and precision.

Delving into the realm of functions, limits, continuity, derivatives, and integrals, Calculus Early Transcendentals, 7th Edition illuminates the intricate interplay between these concepts, revealing their profound significance in shaping our understanding of the physical world. Through real-world examples and thought-provoking exercises, this comprehensive guide fosters a deep comprehension of calculus, equipping readers with the analytical tools necessary to solve real-world problems and make informed decisions.

Introduction

Calculus Early Transcendentals 7th Ed. provides a comprehensive introduction to the fundamental principles of differential and integral calculus. It is designed to equip students with the mathematical tools necessary to analyze and solve problems involving continuous change and motion.The textbook covers a wide range of topics, including:

• Limits and continuity
• Derivatives and their applications
• Integrals and their applications
• Transcendental functions
• Infinite series
• Vector calculus
• Partial differential equations

These concepts are essential for understanding a wide range of phenomena in science, engineering, economics, and other fields.

Purpose of Calculus

Calculus is a powerful mathematical tool that has revolutionized our understanding of the world around us. It has applications in a wide variety of fields, including:

• Physics: Calculus is used to describe the motion of objects, the forces that act on them, and the energy they possess.
• Engineering: Calculus is used to design bridges, buildings, and other structures, as well as to analyze the flow of fluids and the behavior of materials.
• Economics: Calculus is used to model economic growth, predict market trends, and analyze the behavior of consumers and firms.
• Biology: Calculus is used to model the growth of populations, the spread of diseases, and the evolution of species.

Calculus is an essential tool for anyone who wants to understand the world around them and to make informed decisions about the future.

Key Concepts of Calculus

The key concepts of calculus are:

• Limits:Limits are used to describe the behavior of functions as their inputs approach a particular value.
• Derivatives:Derivatives are used to measure the rate of change of functions.
• Integrals:Integrals are used to calculate the area under curves and to find the volume of solids.
• Transcendental functions:Transcendental functions are functions that cannot be expressed in terms of algebraic operations.
• Infinite series:Infinite series are used to represent functions as sums of simpler functions.
• Vector calculus:Vector calculus is used to study functions of several variables.
• Partial differential equations:Partial differential equations are used to model phenomena that involve continuous change in multiple dimensions.

These concepts are the foundation of calculus and are used to solve a wide variety of problems.

Functions and their Graphs

Functions are mathematical relations that assign a unique output value to each input value within a specified domain. Understanding functions and their graphs is crucial in calculus, as they provide a visual representation of the relationship between variables.

Types of Functions

• Linear functionshave a constant rate of change and are represented by straight lines.
• Quadratic functionsare characterized by a parabolic shape and have a turning point.
• Polynomial functionsare composed of terms with non-negative integer exponents and have varying shapes depending on the degree.
• Rational functionsare ratios of polynomial functions and can have vertical and horizontal asymptotes.
• Exponential functionsgrow or decay rapidly and are represented by curves that approach or diverge from the horizontal axis.
• Logarithmic functionsare the inverses of exponential functions and have graphs that are reflections of exponential graphs.
• Trigonometric functionsare periodic functions that represent angles and have characteristic shapes.

Graphing Functions

Functions can be graphed using various techniques:

• Plotting points: Plotting a few points from the function and connecting them with a smooth curve.
• Using intercepts: Finding the x- and y-intercepts and sketching the graph based on their positions.
• Transformations: Applying transformations such as shifts, stretches, or reflections to basic graphs.
• Technology: Using graphing calculators or software to generate accurate graphs.

Applications of Functions

Functions have numerous real-world applications:

• Motion: Describing the position, velocity, and acceleration of objects.
• Growth and decay: Modeling population growth, radioactive decay, and other exponential processes.
• Finance: Calculating interest, annuities, and other financial transactions.
• Physics: Describing relationships between physical quantities, such as force, energy, and momentum.

Limits and Continuity

The concept of limits is fundamental to calculus. A limit describes the value that a function approaches as the input approaches a certain value. Limits are used to define derivatives, integrals, and other important concepts in calculus.

There are several different methods for evaluating limits. One common method is to use algebraic techniques to simplify the expression for the function. Another method is to use L’Hopital’s rule, which can be used to evaluate limits of indeterminate forms.

Continuity, Calculus early transcendentals 7th ed

A function is continuous at a point if its limit at that point is equal to the value of the function at that point. Continuity is an important property of functions, as it ensures that the function can be graphed without any breaks or jumps.

There are several different ways to determine if a function is continuous at a point. One way is to use the epsilon-delta definition of continuity. Another way is to use the following theorem:

If a function is differentiable at a point, then it is continuous at that point.

Derivatives

A derivative is a mathematical operation that measures the rate of change of a function. It is the slope of the tangent line to the graph of a function at a given point. Derivatives have a wide range of applications in various fields, including physics, engineering, economics, and biology.

There are several different methods for finding derivatives, including the limit definition, the power rule, the product rule, and the quotient rule. Each method has its own advantages and disadvantages, and the choice of method depends on the specific function being differentiated.

Geometric Interpretation of Derivatives

The geometric interpretation of a derivative is the slope of the tangent line to the graph of a function at a given point. This slope represents the instantaneous rate of change of the function at that point. For example, the derivative of the position function of an object with respect to time is the velocity of the object, and the derivative of the velocity function with respect to time is the acceleration of the object.

Physical Interpretation of Derivatives

The physical interpretation of a derivative is the rate of change of a physical quantity with respect to another physical quantity. For example, the derivative of the distance function of an object with respect to time is the velocity of the object, and the derivative of the velocity function with respect to time is the acceleration of the object.

Applications of Derivatives

Derivatives have a wide range of applications in various fields, including:

• Physics:Derivatives are used to find the velocity and acceleration of objects in motion, as well as to solve problems involving forces and energy.
• Engineering:Derivatives are used to design and analyze structures, machines, and other engineering systems.
• Economics:Derivatives are used to model and analyze economic systems, including the behavior of markets, firms, and consumers.
• Biology:Derivatives are used to model and analyze biological systems, including the growth and decay of populations, the spread of diseases, and the evolution of species.

Integrals

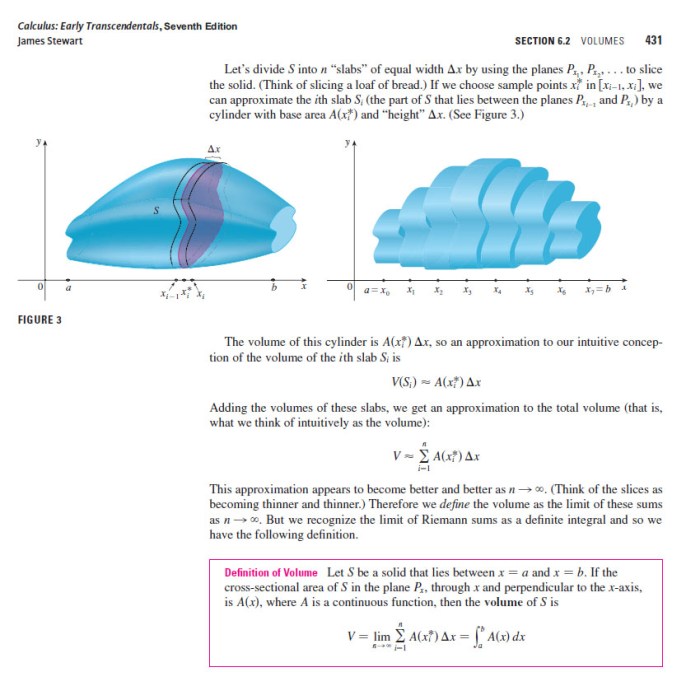
Integrals are mathematical tools used to find the area under a curve, the volume of a solid, and the work done by a force over a distance. They have wide applications in various fields such as physics, engineering, economics, and statistics.

Geometric Interpretation

Geometrically, an integral represents the area under the curve of a function. For a positive function f(x) defined on an interval [a, b], the integral ∫[a, b] f(x) dx gives the area of the region bounded by the graph of f(x), the x-axis, and the vertical lines x = a and x = b.

Physical Interpretation

Physically, an integral can represent the volume of a solid. For a function f(x) defined on an interval [a, b], the integral ∫[a, b] f(x) dx gives the volume of the solid generated by rotating the region under the curve of f(x) about the x-axis.

Methods for Finding Integrals

There are several methods for finding integrals, including:

• The power rule: ∫x^n dx = (x^(n+1))/(n+1) + C
• The substitution rule: ∫f(g(x)) g'(x) dx = ∫f(u) du, where u = g(x)
• The integration by parts rule: ∫u dv = uv – ∫v du
• The trigonometric substitution rule: ∫√(a^2 – x^2) dx = (a/2)arcsin(x/a) + C

Applications of Integrals

Integrals have numerous applications in various fields:

• Physics:Calculating work, energy, and fluid flow
• Engineering:Determining moments of inertia, stresses, and deflections
• Economics:Finding consumer surplus, producer surplus, and elasticity
• Statistics:Calculating probabilities and expected values

Applications of Integration

Integration is a powerful tool that has many applications in science, engineering, and other fields. In this section, we will discuss some of the most common applications of integration, including finding volumes, surface areas, and work.

One of the most important applications of integration is finding the volume of a solid. To find the volume of a solid, we need to integrate the cross-sectional area of the solid with respect to the distance along the axis of revolution.

For example, to find the volume of a sphere, we would integrate the area of a circle with respect to the radius.

Another important application of integration is finding the surface area of a surface. To find the surface area of a surface, we need to integrate the length of the curve that defines the surface with respect to the distance along the curve.

For example, to find the surface area of a sphere, we would integrate the circumference of a circle with respect to the radius.

Finally, integration can also be used to find the work done by a force. To find the work done by a force, we need to integrate the force with respect to the distance over which the force is applied. For example, to find the work done by a constant force over a distance, we would integrate the force with respect to the distance.

Examples of Real-World Problems that can be Solved Using Integration

• Finding the volume of a water tank
• Finding the surface area of a car
• Finding the work done by a motor
• Finding the center of mass of an object
• Finding the moment of inertia of an object

Differential Equations

Differential equations are mathematical equations that involve an unknown function and its derivatives. They play a crucial role in various fields of science, engineering, and economics.

Differential equations describe how a quantity changes with respect to another quantity. They arise naturally when modeling phenomena that involve rates of change, such as the growth of populations, the motion of objects, or the flow of fluids.

Methods for Solving Differential Equations

There are various methods for solving differential equations, including:

• Analytical methods: These involve finding an explicit solution to the equation in terms of elementary functions.
• Numerical methods: These approximate the solution using numerical techniques, such as Euler’s method or the Runge-Kutta method.
• Graphical methods: These involve plotting the direction field of the equation and using it to sketch the solution curves.

Applications of Differential Equations

Differential equations have a wide range of applications in various fields:

• Population growth: Differential equations model the growth and decline of populations, taking into account factors such as birth rates, death rates, and migration.
• Motion of objects: Differential equations describe the motion of objects under the influence of forces, such as gravity or friction.
• Fluid flow: Differential equations govern the flow of fluids, such as water or air, and are used in the design of pipelines, pumps, and other fluid systems.
• Electrical circuits: Differential equations model the behavior of electrical circuits, including the flow of current and the voltage across components.
• Economics: Differential equations are used to model economic phenomena, such as the growth of economies, the dynamics of supply and demand, and the pricing of financial instruments.

Infinite Series

An infinite series is an expression of the form$$\sum_n=1^\infty a_n = a_1 + a_2 + a_3 + \cdots$$where each a_nis a real number.An infinite series is said to converge if the sequence of partial sums$$s_n = \sum_i=1^n a_i = a_1 + a_2 + a_3 + \cdots + a_n$$converges to a finite number L. If the sequence of partial sums diverges, then the infinite series is said to diverge.There

are several tests that can be used to determine whether an infinite series converges or diverges. Some of the most common tests include:

• The Ratio Test
• The Root Test
• The Comparison Test
• The Integral Test

Infinite series have many applications in mathematics, science, and engineering. Some of the most common applications include:

• Representing periodic functions as Fourier series
• Solving differential equations
• Approximating integrals
• Calculating probabilities

Multivariable Calculus: Calculus Early Transcendentals 7th Ed

Multivariable calculus extends the concepts of single-variable calculus to functions of multiple variables. It introduces the ideas of partial derivatives, multiple integrals, and vector calculus.

Multivariable calculus has wide applications in various fields, including physics, engineering, economics, and data science.

Functions of Several Variables

Functions of several variables are functions whose inputs are tuples of numbers and whose outputs are single numbers. For example, the function \(f(x, y) = x^2 + y^2\) takes two inputs, \(x\) and \(y\), and outputs the sum of their squares.

Partial Derivatives

Partial derivatives are derivatives of functions of several variables with respect to one variable while holding the other variables constant. For example, the partial derivative of \(f(x, y) = x^2 + y^2\) with respect to \(x\) is \(\frac\partial f\partial x = 2x\).

Multiple Integrals

Multiple integrals are integrals of functions of several variables over multidimensional regions. For example, the double integral of \(f(x, y) = x^2 + y^2\) over the rectangle \(R = [0, 1] \times [0, 1]\) is \(\iint_R (x^2 + y^2) dA = \frac13\).

Clarifying Questions

What are the key concepts covered in Calculus Early Transcendentals, 7th Edition?

Calculus Early Transcendentals, 7th Edition delves into the fundamental concepts of calculus, including functions, limits, continuity, derivatives, integrals, and their applications in various fields.

How does Calculus Early Transcendentals, 7th Edition approach the teaching of calculus?

Calculus Early Transcendentals, 7th Edition adopts a rigorous and comprehensive approach, providing a solid foundation in the principles of calculus through clear explanations, ample practice problems, and real-world applications.

What are the benefits of using Calculus Early Transcendentals, 7th Edition as a textbook?

Calculus Early Transcendentals, 7th Edition empowers students with a deep understanding of calculus, equipping them with the analytical tools and problem-solving skills essential for success in STEM fields and beyond.